Deviační moment symetrických těles
Vzorec pro výpočet deviačního momentu setrvačnosti k osám y,z:
1.1. Dyz = Int2 (yz)dA
kde Int2 je dvojný integrál, dA=dxdy a je to plošný element 2D obrazce A
Deviační moment nabývá kladných, záporných či nulových hodnot, jak je zřejmé již ze samotné
definice deviačního momentu.
Hlavní osy setrvačnosti jsou takové osy y,z, ke kterým vychází deviační moment roven nule.
Deviační moment je roven nule k ose souměrnosti tělesa, tj. pro symetrické těleso, kdy v jedné
ose symetrie leží osa, ke které počítáme deviační moment. A to platí pro těleso které má
stejnou hustotu ve všech bodech či má tuto hustotu souměrně rozloženou k ose souměrnosti.
Deviační moment tělesa symetrického v 1 nebo více směrech (např. půlkruh - 1 směr, obdélník
a elipsa - 2 směry, čtverec - 4 směry, kruh - nekonečno směrů.) je roven tedy vždy nule,
pokud prochází alespoň jedna z os ke kterým počítáme deviační moment osou symetrie tělesa.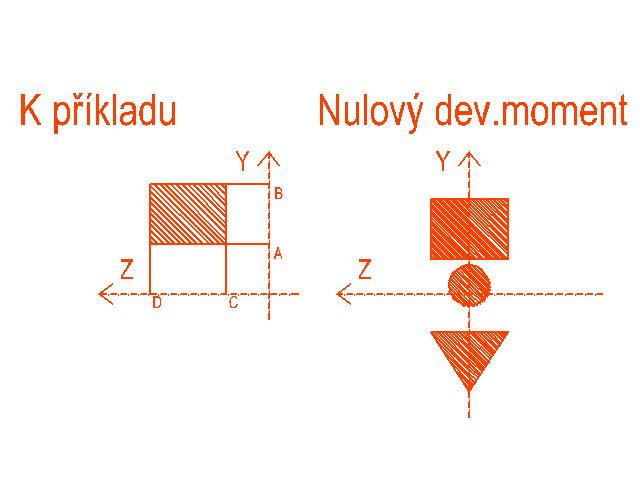
Abych vám moc nezamotal hlavu, nebudu příliš rozepisovat teorii, ikdyž je jednoduchá a vyplývá
ze vzorce 1.1.
Příklad na deviační moment:
Odvodíme si deviační moment setrvačnosti obdélníku v kartézké souřadnicové soustavě y, z,
která má strany rovnoběžné se souřadnicovými osami y, z. Na ose y bude obdélník vymezen
body A a B, přičemž A < B a podobně na ose z je obdélník vymezen body C a D, kde C < D.
Dle 1.1. začneme s obecným výpočtem :
vysvětlivky: [x=i,j] jsou definované meze integrálu na ose x, i < j
Dyz = Int2 (yz)dA = Int dz[z=C,D] Int dy[y=A,B] (y.z) = Int dz[z=C,D] (1/2 . z . y^2 [y=A,B])=
= (B^2 - A^2) /2 . Int dz[z=C,D] (z) = (B^2 - A^2) /4 . (z^2 [z=C,D])=
= (B^2 - A^2) . (D^2 - C^2) / 4
Z tohoto vzorce je zřejmé, že pokud např. osa y, ke které budeme počítat deviační moment bude
procházet v ose symetrie obdélníku ... tj. ve prostřed strany obdélníku mezi body C a D, potom
celý deviační moment je roven nule.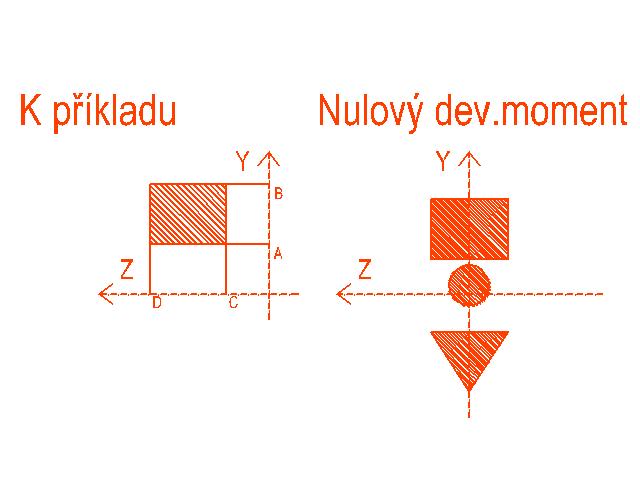
Přečteno:17128
Autor: David Mizera