Moment setrvačnosti obdélníku v 2D

Kategorie >>Věda a technika>> Moment setrvačnosti obdélníku v 2D

Poslední dobou sem se ve škole setkal se zbytečným nešvarem a to ve výpočtech momentu setrvačnosti k nějaký vose.

Vezmu ten nejjednodušší případ a to je výpočet momentu setrvačnosti složenýho rovinnýho vobrazce z obdélníků. Všichni jsou tupě a trošku zbytečně naučený použít pro každou část rovinnýho obrazce – v tomle případě pro každej obdélníček moment setrvačnosti k centrální ose (tj. moment setrvačnosti, k vose procházející těžištěm rovinnýho vobrazce) a připočíst k němu Steinerův doplněk (ten kompenzuje vzdálenost skutečný polohy jednotlivýho vobdélníčku od celýho těžiště rovinnýho tělesa).

Takže to vypadá zhruba takle: moment setrvačnosti vobdélníku se k těžišťový vose např. y spočte jednoduše :

I_y1 = 1/12 . b . h³

kde

b je rovnobježná strana k těžišťový vose y

h je srana vobdélníku kolmá na y

a k tomu se přidá Steinerův doplněk :

I_y2 = A . r²

kde

A je plocha vobdélníku (A=b.h)

r je vzdálenost těžiště tajitoho vobdélníku vod vosy y, prakticky to je vzdálenost osy y vod půlky hrany “h” kolmý na vosu y

Takže celkovej vzorec vypadá následovně :

I_y = 1/12 b.h³ + bh.r²

No a vezměme to vobecněji, aby každej viděl možnej postup, jak si to zjistit sám a bez naučených vzorců, ikdyž popravdě de vo jedno a o samý.

Moment setrvačnosti je definovanej na oblasti Ω asi zhruba přesně následovně:

I_y = ∫∫z² dΩ

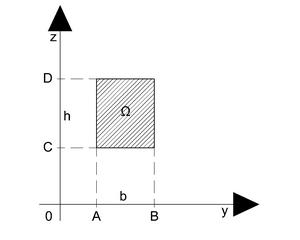
Nakeslíš si vobdélník do nějaký ortogonální soustavy souřadnic, takže ta bude mít dejme tomu vosu y kolmou na vosu z.

Tak dvojnej integrál se v tomle případě počítá hodně jednoduše – ještě si vzmezíme meze vobdélníku a tak... budeme počítat moment setrvačnosti k vose y. Na vose y si poznačíme vzdálenosti A,B; A < B, což sou body vobdélníku promítnutý na vosu y z hrany s toule vosou rovnoběžný.

Ok a na vosu z, kerá je k vose y kolmá jak sviň si promítneš body C a D, zase C < D a taky to je rovnoběžná hrana k vose – ale k vose z.

Ok a tím máme vymezený hranice integrálu.

Výpočet je jednoduchej a to:

I_y = ∫∫z² dΩ = ∫∫z² dydz =

= ∫[A,^B]dy ∫[_C, ^D] z²dz =

= 1/3 . ∫[A,^B]dy (D³-C³) =

= (D³-C³)/3 . (y)[_A, ^B] =

= (B-A)(D³-C³)/3 =

= b(D³-C³)/3

I_y= (B-A)(D³-C³)/3 = b(D³-C³)/3

kde h je strana rovnobježná s osou momentu setrvačnosti.

Čest mechanice