Obsah pravoúhlého trojúhelníku pomocí dvojného integrálu

Máme zadán trojúhelník ABC:

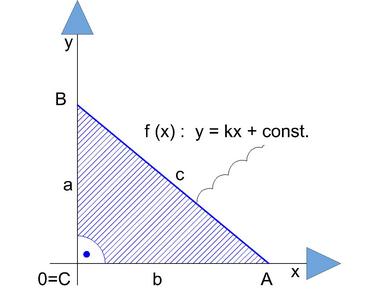
A[x_A,0], pro zjednodušení poruším pravidla a označím dle obrázku: A[A,0]

B[0,y_B], také B[0,B]

C[0,0]

Nejprve dosadíme do funkce přímky: y = kx + const.

bod B: x = 0 : y = B, potom B = k.0 + const.

const. = B

bod A: y = 0 : x = A, potom 0 = k.A + B

odtud:

k = -B/A

potom tedy rovnice přímky:

y = -(B/A) . x + B

Pro výpočet obsahu pravoúhlého trojuhelníku použijeme dvojný integrál z 1 (hustota =1).

S = ∫∫ dx dy = ∫[₀,^A]dx ∫[₀, ^{-B/A.x + B}]dy =

= ∫[₀,^A] (-B/A . x +B)dx = [-(B/2A) . x² + Bx]₀^A=

=-AB/1 + AB

S = AB/2

kde např. [₀,^A] .. 0 je dolní mez integrálu a A je horní mez integrálu

tedy to samo jako známý vzorec S = a . v_a / 2

přičemž v pravoúhlém trojúhelníku je v_a = b

Komentáře (0)