Obsah lichoběžníku pomocí dvojného integrálu
Máme zadán lichoběžník 0HAB, potřebujeme spočítat jeho obsah:
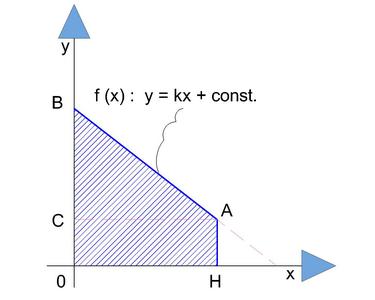
Body lichoběžníku 0HAB, zjednodušený zápis bez indexů..:
0[0,0]
H[H,0]
A[C,H]
B[0,B]
Nejprve zjistime rovnici přímky AB:
y = kx + const.
bod B: x = 0 : y = B, potom y = kx + B
bod A: x = H : y = C, potom C = kH + B
z toho:
k = (C - B) / H
Rovnice AB:
y = x . (C - B) / H + B
Pro výpočet obsahu lichoběžníku použijeme dvojný integrál z 1 (hustota =1).
S = ∫∫ dx dy = ∫[0,H]dx ∫[0, (C-B)/H.x + B]dy =
= ∫[0,H] ( (C-B)/H . x + B ) dx = [(C - B )/ 2H . x2 + Bx]0H=
= (C - B) . H /2 + BH = H . (C+B) / 2
obsahu lichoběžníku:
S = H . (C+B) / 2
Kontrola.. součet obsahů obdédlíku AC0H a obsahu trojúhelníku ACB:
S = CH + (B - C) . H / 2 = H (C -C/2 +B/2) = H (C + B) / 2, takže souhlasí s výpočterm..
kde např. [0,A] .. 0 je dolní mez integrálu a A je horní mez integrálu
tedy to samo jako známý vzorec S = a . va / 2
přičemž v pravoúhlém trojúhelníku je va = b
Souvisejicí články
| Tabulka po 1º sin(x), sin(2x),sin2(x),cos(x),cos(2x),cos2(x),tg(x),tg(2x).. | Hodnoty goniometrických funkcí |
| Hyperbolické funkce - sinh, cosh, tgh, arctgh, sech, cosech | |
| Pravoúhlý trojúhelník rovnoramenný- vlastnosti | |
| Velikost úsečky v prostrou | |
| Kruh o stejném obsahu jako čtverec | |
| Pythagorova věta | Pythagorova věta s obrázkem |
| Tabulka elementárních derivací | |
| Deviační moment pravoúhlého trojúhelníku | Výpočet pomocí dvojného integrálu |
| Moment setrvačnosti pravoúhlého trojúhelníku | Výpočet pomocí dvojného integrálu |
| Obsah pravoúhlého trojúhelníku pomocí dvojného integrálu | Odvození známeho vzorce pro obsah trojúhelníku |
| Goniometrické funkce násobků a poloviny argumentu | sin2x, sin3x,sin4x, cos2x,cos3x,... |
| Vztahy mezi goniometrickými funkcemi stejného argumentu | tg, cotg, sin, cos |
| Znaménka hodnot goniometrických funkcí v kvadrantech | |
| Definice goniometrických funkcí na pravúhlém trojúhelníku | sin, cos, tg, cotg, sec, cosec |
| Hodnoty goniometrických funkcí pro význačné úhly | Tabulka vyčíslených hodnot. |
| Odvození tečny ke kružnici - Thaletova věta | 1) Thaletova věta, 2) rovnice přimky a kružnice |
| Funkce sinus a cosinus | v oboru reálných čísel |
Vloženo: 25.12.2008 14:57
Přečteno:8261
Autor: David Mizera
Hlasů: 6
Hodnocení(jako ve škole): 3.17
-
Nový Komentář
