Pravoúhlý trojúhelník rovnoramenný- vlastnosti
Speciální případ trojúhelníku - rovnoramenný pravoúhlý trojúhleník.
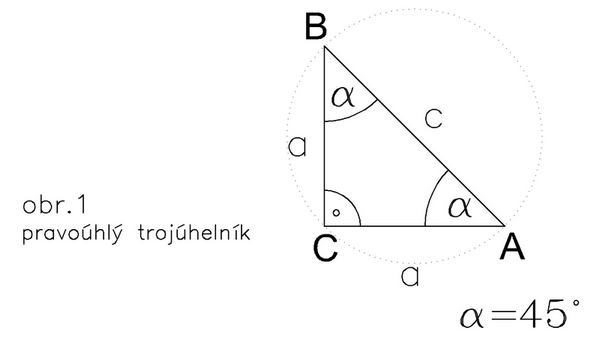
Obvod rovnoramenného pravoúhlého trojúhleníku ABC:
o = 2a +c
taktéž Pythagorova věta : a2 + b2 = c2
kde a=b : c=√(2a2) = a√2
o = 2a + a√2
o = a( 2+√2)
a přibližně: o ≈ 3.414214a
Obsah rovnoramenného pravoúhlého trojúhleníku ABC:
S= a . va /2
S = a2/2
dále je možné vyjádřit obsah pomocí obvodu - abychom viděli závislost
nejprve odvodíme a a rozšíříme zlomek v čitateli i jmenovateli o ( 2-√2) :
a = o/( 2+√2) = o( 2-√2)/(4-2)
a = o(2-√2) / 2
S = o2 . (2-√2)2/8
S ≈ 0,0428932 o
lektor : PJK
Souvisejicí články
| Tabulka po 1º sin(x), sin(2x),sin2(x),cos(x),cos(2x),cos2(x),tg(x),tg(2x).. | Hodnoty goniometrických funkcí |
| Hyperbolické funkce - sinh, cosh, tgh, arctgh, sech, cosech | |
| Velikost úsečky v prostrou | |
| Kruh o stejném obsahu jako čtverec | |
| Pythagorova věta | Pythagorova věta s obrázkem |
| Tabulka elementárních derivací | |
| Deviační moment pravoúhlého trojúhelníku | Výpočet pomocí dvojného integrálu |
| Moment setrvačnosti pravoúhlého trojúhelníku | Výpočet pomocí dvojného integrálu |
| Obsah lichoběžníku pomocí dvojného integrálu | Odvození vzorce pro obsah lichoběžníku |
| Obsah pravoúhlého trojúhelníku pomocí dvojného integrálu | Odvození známeho vzorce pro obsah trojúhelníku |
| Goniometrické funkce násobků a poloviny argumentu | sin2x, sin3x,sin4x, cos2x,cos3x,... |
| Vztahy mezi goniometrickými funkcemi stejného argumentu | tg, cotg, sin, cos |
| Znaménka hodnot goniometrických funkcí v kvadrantech | |
| Definice goniometrických funkcí na pravúhlém trojúhelníku | sin, cos, tg, cotg, sec, cosec |
| Hodnoty goniometrických funkcí pro význačné úhly | Tabulka vyčíslených hodnot. |
| Odvození tečny ke kružnici - Thaletova věta | 1) Thaletova věta, 2) rovnice přimky a kružnice |
| Funkce sinus a cosinus | v oboru reálných čísel |
Vloženo: 19.01.2012 22:59
Přečteno:56288
Autor: dm
Hlasů: 49
Hodnocení(jako ve škole): 3.22
-
Nový Komentář
Autor:
kesch
Datum:
12.04.2012 21:14:09
Autor:
dm
Datum:
23.04.2012 15:31:17
ahaaaa...to ses ty ,kez ? 

