Moment setrvačnosti pravoúhlého trojúhelníku
Odvodíme si vzorec pro výpočet momentu setrvačnosti pravoúhlého trojúhelníku dle obrázku. Jedná se o speciální případ, kdy trojúhelník leží stranou na ose otáčení. Pro ilustraci ideální začátek, později spočteme moment setrvačnosti trojúhelníku ležící jakkoli daloko od osy či na ose..
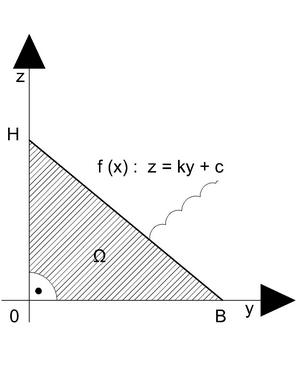
Nejprve dosadíme do funkce přímky: z = ky + c
k = -H/B
c = H
a tedy rovnice přímky HB ohraničující oblast je:
z = - H/B . y + H
Definice momentu setrvačnosti:
Iy = ∫∫z2 dΩ
kde Ω je oblast, zde trojúhelník 0BH
Moment výpočet momentu setrvačnosti trojúhelníku jednotkové hustoty či hmotnosti 0BH:
Iy = ∫∫z2 dΩ =
= 1/3 . ∫[0,B]dy ∫[0, -H/B.y + H] z2 dz =
= 1/3 . ∫[0,B] (-H/B . y + H)³ dy =
= H³/3 . ∫[0,B] (1 - 3y/B + 3y²/B² - y³/B³)dy =
= H³/3 .[y - 3y²/2B + y³/B² - y4/4B³] [0,B] =
Iy = BH3/12
kde
[0,B], [0, -H/B.y + H] .. meze integrálu
Souvisejicí články
| Tabulka po 1º sin(x), sin(2x),sin2(x),cos(x),cos(2x),cos2(x),tg(x),tg(2x).. | Hodnoty goniometrických funkcí |
| Hyperbolické funkce - sinh, cosh, tgh, arctgh, sech, cosech | |
| Pravoúhlý trojúhelník rovnoramenný- vlastnosti | |
| Velikost úsečky v prostrou | |
| Kruh o stejném obsahu jako čtverec | |
| Pythagorova věta | Pythagorova věta s obrázkem |
| Tabulka elementárních derivací | |
| Deviační moment pravoúhlého trojúhelníku | Výpočet pomocí dvojného integrálu |
| Obsah lichoběžníku pomocí dvojného integrálu | Odvození vzorce pro obsah lichoběžníku |
| Obsah pravoúhlého trojúhelníku pomocí dvojného integrálu | Odvození známeho vzorce pro obsah trojúhelníku |
| Goniometrické funkce násobků a poloviny argumentu | sin2x, sin3x,sin4x, cos2x,cos3x,... |
| Vztahy mezi goniometrickými funkcemi stejného argumentu | tg, cotg, sin, cos |
| Znaménka hodnot goniometrických funkcí v kvadrantech | |
| Definice goniometrických funkcí na pravúhlém trojúhelníku | sin, cos, tg, cotg, sec, cosec |
| Hodnoty goniometrických funkcí pro význačné úhly | Tabulka vyčíslených hodnot. |
| Odvození tečny ke kružnici - Thaletova věta | 1) Thaletova věta, 2) rovnice přimky a kružnice |
| Funkce sinus a cosinus | v oboru reálných čísel |
Vloženo: 27.12.2008 12:39
Přečteno:8330
Autor: David Mizera
Hlasů: 8
Hodnocení(jako ve škole): 3.88
-
Nový Komentář
